7.4 正交试验法
7.4.1 基本概念
正交试验设计(Orthogonal experimental design)是研究多因素多水平的设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点。正交试验设计基于正交表,效率高、快速、经济,核心思想是用最小的测试用例集合获得最大的测试覆盖率。
所有参与试验、影响试验结果的条件称为因素。试验因素的取值或输入叫做因素的水平。
正交表是经过试验得到的数据表,它有如下的构成:
行数(Runs):正交表中行的个数,即试验的次数。
因素数(Factors):正交表中列的个数。
水平数(Levels):任何单个因素能够取得的值的最大个数。正交表中的包含的值为从0到“水平数-1”或从1到“水平数”。
正交表的表示形式:
正交表举例:
3因素,每个因素2水平,结果4行:
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 |
| 3 | 2 | 1 | 2 |
| 4 | 2 | 2 | 1 |
4因素,每个因素3水平,结果9行:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 2 | 1 | 2 | 3 |
| 5 | 2 | 2 | 3 | 1 |
| 6 | 2 | 3 | 1 | 2 |
| 7 | 3 | 1 | 3 | 2 |
| 8 | 3 | 2 | 1 | 3 |
| 9 | 3 | 3 | 2 | 1 |
整齐可比性:在同一张正交表中,每个因素的每个水平出现的次数是完全相同的。
均衡分散性:在同一张正交表中,任意两列(两个因素)的水平搭配(横向形成的数字对)是完全相同的。
7.4.2 步骤
根据需求分析有哪些因素(变量);每个因素有几个水平(变量的取值);
选择一个合适的正交表;
如何选择合适的正交表?
- 考虑因素(变量)的个数
- 考虑因素水平(变量的取值)的个数
- 考虑正交表的行数:取行数最少的一个
把变量的值映射到表中;
把每一行的各因素水平的组合做为一个测试用例;
加上认为可疑且没有在表中出现的组合。
7.4.3 举例
1.因素数(变量)、水平数(变量值)相符
假设查询某个人时有三个查询条件:
- 根据“姓名”进行查询。
- 根据“身份证号码”查询。
- 根据“手机号码”查询。
考虑查询条件要么不填写,要么填写,此时可用正交表进行设计。
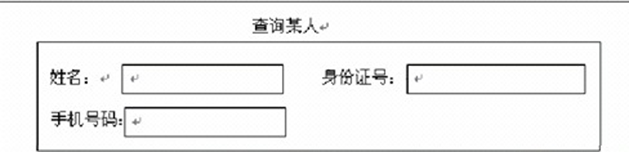
有三个因素:
姓名、身份证号、手机号码
每个因素有两个水平:
姓名:填、不填
身份证号:填、不填
手机号码:填、不填
选择:
映射正交表:
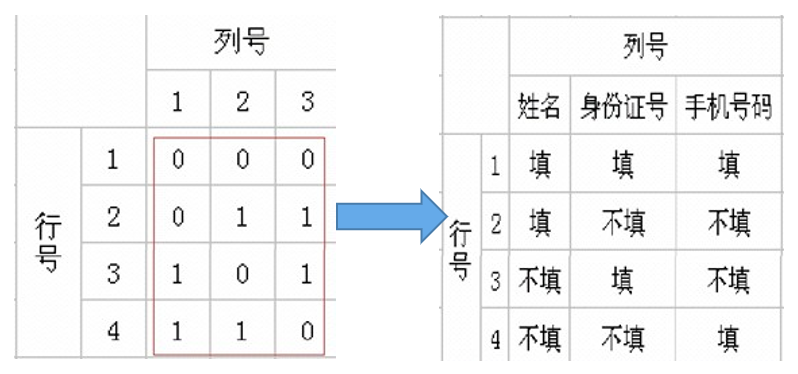
生成测试用例如下:
1:填写姓名、填写身份证号、填写手机号
2:填写姓名、不填身份证号、不填手机号
3:不填姓名、填写身份证号、不填手机号
4:不填姓名、不填身份证号、填写手机号
增补测试用例:
5:不填姓名、不填身份证号、不填手机号
测试用例减少数:8 -> 5
2.因素数(变量)不相同
水平数(变量的取值)相同但在正交表中找不到相同的因素数(变量),取因素数最接近但略大于实际值的表。
114查询系统:
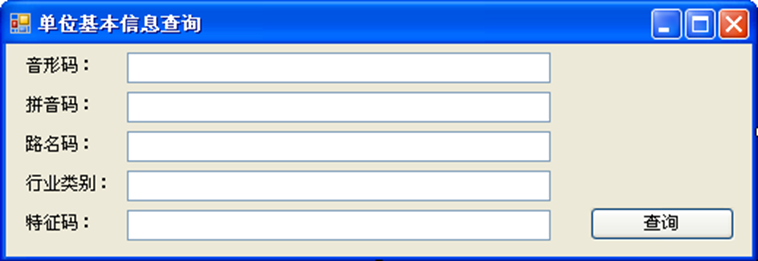
分析因素数和水平数:
有五个因素:
音形码、拼音码、路名码、行业类别和特征码
每个因素有两个水平:
音形码:填、不填
拼音码:填、不填
路名码:填、不填
行业类别:填、不填
特征码:填、不填
选择正交表:
表中的因素数>= 5
表中至少有五个因素的水平数>= 2
行数取最少的一个
结果:
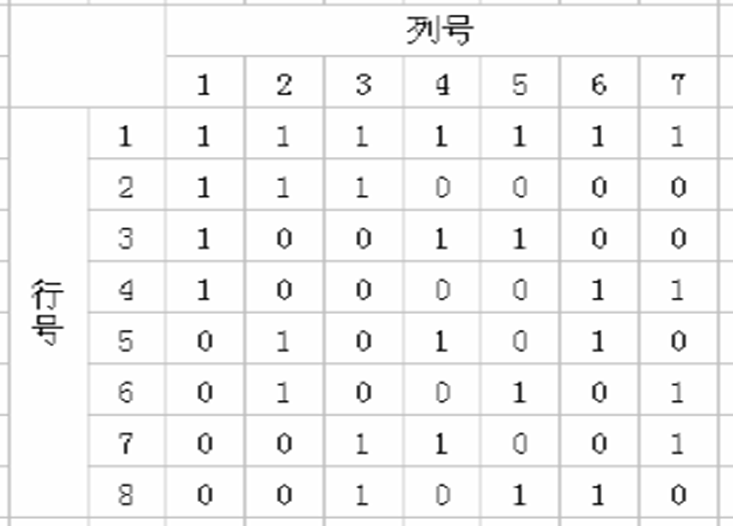
映射正交表,舍弃没有使用的因素列:
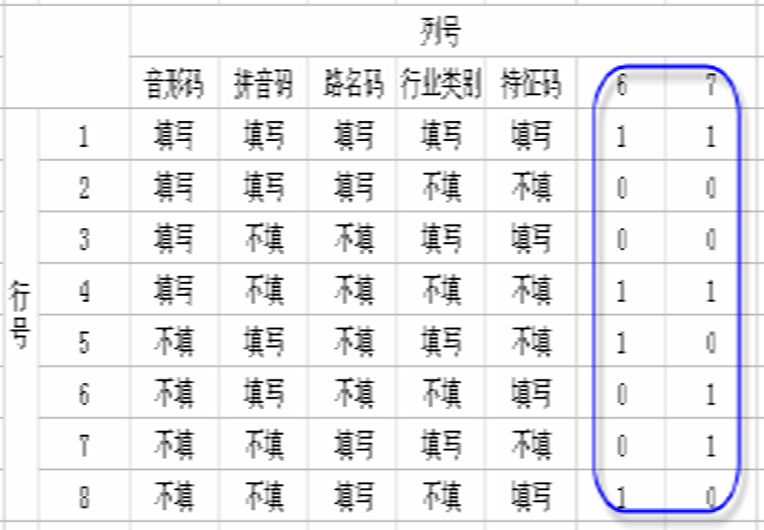
生成生成测试用例:
用 设计的测试用例如下:
音形码填写、拼音码填写、路名码填写、行业类别填写、特征码填写
音形码填写、拼音码填写、路名码填写、行业类别不填、特征码不填
音形码填写、拼音码不填、路名码不填、行业类别填写、特征码填写
音形码填写、拼音码不填、路名码不填、行业类别不填、特征码不填(重复)
音形码不填、拼音码填写、路名码不填、行业类别填写、特征码不填
音形码不填、拼音码填写、路名码不填、行业类别不填、特征码填写
音形码不填、拼音码不填、路名码填写、行业类别填写、特征码不填
音形码不填、拼音码不填、路名码填写、行业类别不填、特征码填写
增补测试用例:
音形码填写、拼音码不填、路名码不填、行业类别不填、特征码不填(与上面重复,舍弃)
音形码不填、拼音码填写、路名码不填、行业类别不填、特征码不填
音形码不填、拼音码不填、路名码填写、行业类别不填、特征码不填
音形码不填、拼音码不填、路名码不填、行业类别填写、特征码不填
音形码不填、拼音码不填、路名码不填、行业类别不填、特征码填写
音形码不填、拼音码不填、路名码不填、行业类别不填、特征码不填
测试用例减少数: 32 -> 13
3.水平数(变量值)不相同
因素(变量)的水平数(变量的取值)不相同。
水平数不相同的情况:
假设一个系统有5个独立的变量( A,B,C,D,E)。
变量A和B都有两个可能的取值(A1,A2;B1,B2 )。
变量C和D都有三个可能的取值( C1,C2,C3 ;D1,D2,D3 )。
变量E有六个可能的取值(E1,E2,E3,E4,E5,E6 )。
有五个因素(变量),两个因素有两个水平(变量的取值)、两个因素有三个水平,一个因素有六个水平:
A:A1、A2
B:B1、B2
C:C1、C2、C3
D:D1、D2、D3
E:E1、E2、E3、E4、E5、E6
选择正交表:
表中的因素数(变量) >= 5
表中至少有二个因素的水平数(变量的取值)>= 2
至少有另外二个因素的水平数>= 3
还至少有另外一个因素的水平数>= 6
行数取最少的一个( 、 )
结果:
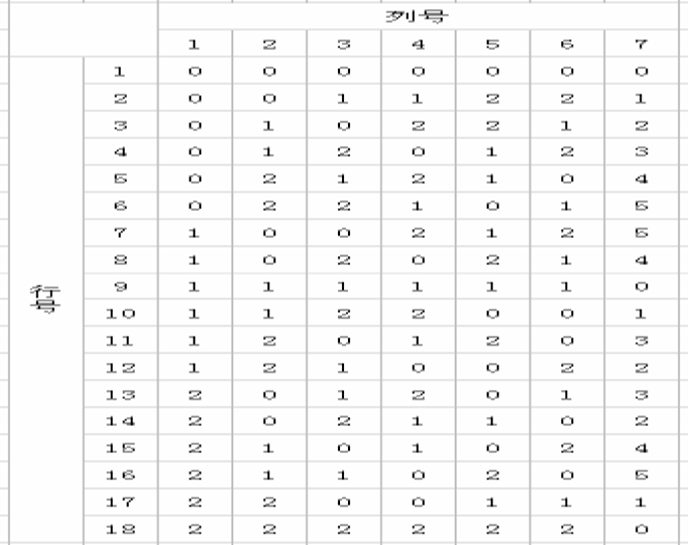
映射正交表:
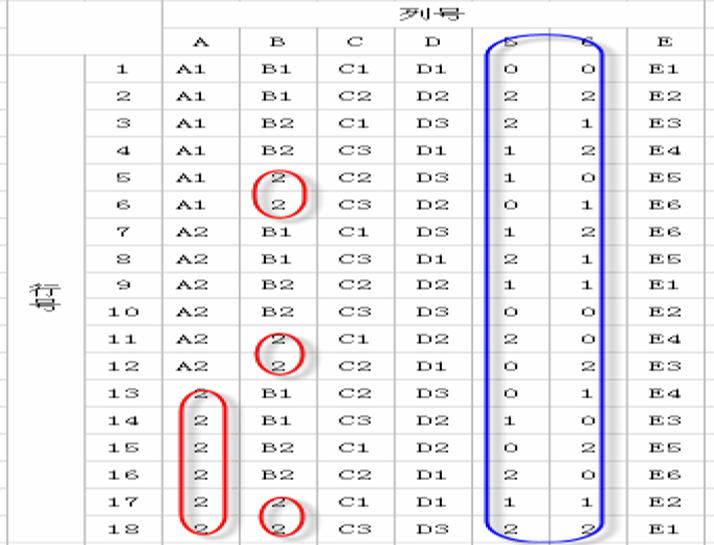
舍弃没有使用的因素列,对于一些因素中多余的水平,可以按照平均分配的方法赋予这个因素的水平值,最后去除可能产生的重复行。
生成生成测试用例(略):
测试用例减少数: 216 -> 18
7.4.4 练习
1.假设一个WEB站点,对该站点进行兼容性测试,需要考虑:
WEB浏览器:Chrome、FireFox、Safari
操作系统:Windows 10、macOS、Ubuntu
应用服务器:IIS、Apache、Nginx
数据库:Oracle、MySQL、PostgreSQL
2.PowerPoint软件打印功能可以设置如下打印选项:
打印范围分:全部、当前幻灯片、给定范围
打印内容分:幻灯片、讲义、备注页、大纲视图
打印颜色/灰度分: 颜色、灰度、黑白
打印效果分:幻灯片加框、幻灯片不加框
7.4.5 其他方式
1.当水平值不一致的时候,也可以选取水平值较多的那个。
确定水平值之后,如果没有合适的正交表,依次增加因素数和水平数,如果有多个正交表都合适,选取行数较少的那个。
当确定完正交表,但是其中部分水平值多或者少的情况:
少:多出来的水平值用存在的任意值任意替换。
多:将多出来的与其中一个结合起来去写,写完之后再进行拆分。
然后补充极端情况,再把具体业务对照写入正交表,最后编写测试用例(每一行一条用例)。
2.allpairs方法
先把因子和水平在Excel表中编辑好,复制出来到一个txt文档中,然后使用命令:
allpairs.exe in.txt > out.txt
即可得到正交表和用例组合。
3.在线SPSSAU方法
在https://spssau.com/indexs.html 的正交实验中可以自动生成正交表,然后再对生成结果进行处理。
4.获取正交表